SPSS 因子分析 - 中级教程

作者：Ruben Geert van den Berg，发表于 因子分析 栏目下。

哪些性格特质可以预测职业抱负？一项研究旨在回答这个问题。数据（部分如下所示）位于 20-career-ambitions-pca.sav 文件中。

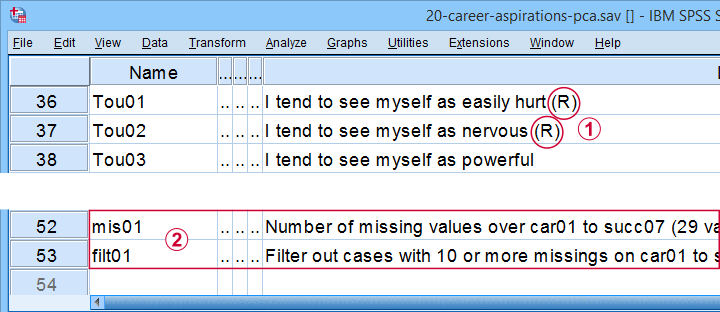
SPSS Factor Analysis Promax Rotation Variable View

变量 Car01（“career ambitions（职业抱负）”的缩写）到 Succ07（“successfulness（成功）”的缩写）试图衡量 5 种特质。这些变量已经为分析做好了准备：

一些负面陈述被进行了 反向编码，因此在其变量标签后附加了“(R)”; mis01 包含了每个受访者的 缺失值 的数量。我们创建了 filt01，它会过滤掉任何在 29 个变量中有 10 个或更多缺失值的受访者。

我们现在想要回答的第一个研究问题是：

  • 这 29 个陈述是否确实衡量了 5 个潜在的特质或“因素”？
  • 哪些陈述精确地衡量了哪些因素？

因子分析将精确地回答这些问题。但首先，让我们通过运行以下 语法 来激活我们的筛选变量。

***Activate filter variable.
** filter by filt01.

***Inspect missing values per respondent.
** frequencies mis01.

结果

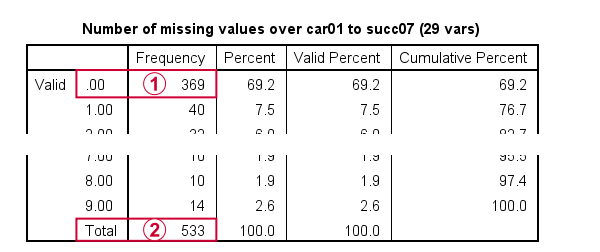
SPSS Factor Analysis Inspect Missing Values

请注意，在 N = 575 个案例中，只有 369 个案例在所有 29 个变量上都有零缺失值。 通过我们的 FILTER 命令，所有分析将仅限于 N = 533 个具有 9 个或更少缺失值的案例。现在，根据经验法则，我们希望在因子分析中为每个变量至少使用 15 个案例。因此，对于我们的示例分析，我们希望至少使用 29（变量）* 15 = 435 个案例。这是包含一些不完整受访者的原因之一。另一个原因是更大的样本量会导致更大的 统计功效 和更小的 置信区间。

好的。我们现在准备好了，让我们继续进行实际的因子分析。

SPSS 因子分析对话框

首先，让我们从 A nalyze（分析） SPSS Menu Arrow D imension Reduction（降维） SPSS Menu Arrow F actor（因子） 打开因子分析对话框，如下所示。

SPSS Analyze Dimension Reduction Factor

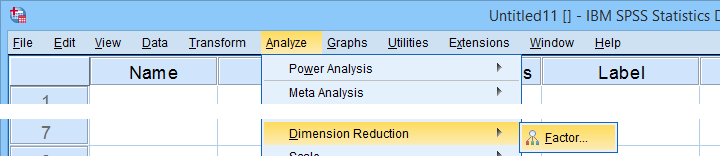
对于我们的第一次分析，大多数默认设置都可以。但是，我们确实想调整 Rotation（旋转） 和 Options（选项） 下的一些设置。

SPSS Factor Analysis Dialogs

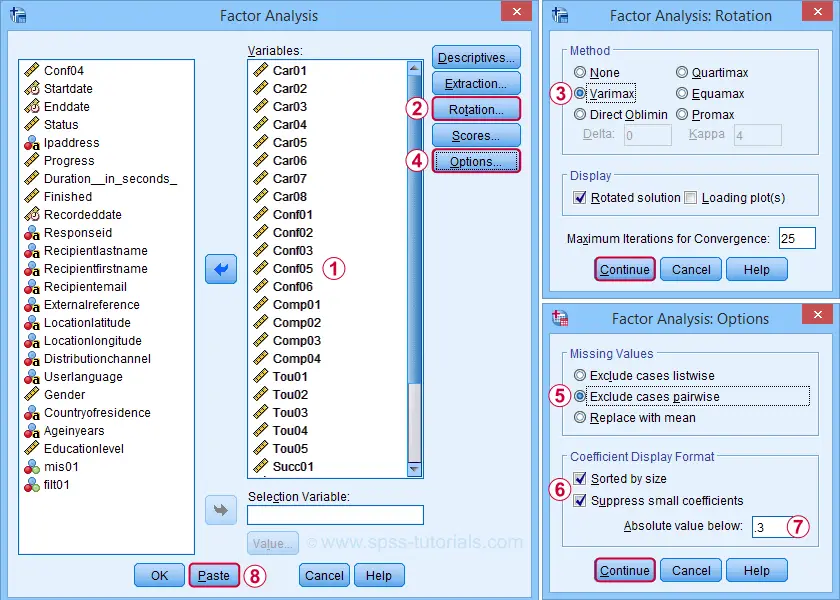
我们将成对排除具有缺失值的案例。Listwise（列表式）排除将我们的分析限制为 N = 369 个完整案例，这对于 29 个变量来说（可以说）样本量不足。

完成这些步骤会产生以下语法。

SPSS FACTOR 语法 I - 基本设置

***PCA I - BASIC SETTINGS.
**
FACTOR
/VARIABLES Car01 Car02 Car03 Car04 Car05 Car06 Car07 Car08 Conf01 Conf02
Conf03 Conf05 Conf06
Comp01 Comp02 Comp03 Comp04 Tou01 Tou02 Tou03 Tou04 Tou05 Succ01 Succ02 Succ03
Succ04 Succ05 Succ06
Succ07
/MISSING PAIRWISE
/ANALYSIS Car01 Car02 Car03 Car04 Car05 Car06 Car07 Car08 Conf01 Conf02 Conf03
Conf05 Conf06
Comp01 Comp02 Comp03 Comp04 Tou01 Tou02 Tou03 Tou04 Tou05 Succ01 Succ02 Succ03
Succ04 Succ05 Succ06
Succ07
/PRINT INITIAL EXTRACTION ROTATION
/FORMAT SORT BLANK(.3)
/CRITERIA MINEIGEN(1) ITERATE(25)
/EXTRACTION PC
/CRITERIA ITERATE(25)
/ROTATION VARIMAX
/METHOD=CORRELATION.

在此语法中，ANALYSIS 和第二个 CRITERIA 子命令是多余的。删除它们可以保持语法整洁，并使其更容易复制粘贴编辑以进行后续分析。因此，我更喜欢使用下面的缩短语法。

***PCA I - BASIC SETTINGS.
**
FACTOR
/VARIABLES Car01 Car02 Car03 Car04 Car05 Car06 Car07 Car08 Conf01 Conf02
Conf03 Conf05 Conf06
Comp01 Comp02 Comp03 Comp04 Tou01 Tou02 Tou03 Tou04 Tou05 Succ01 Succ02 Succ03
Succ04 Succ05 Succ06
Succ07
/MISSING PAIRWISE
/PRINT INITIAL EXTRACTION ROTATION
/FORMAT SORT BLANK(.3)
/CRITERIA MINEIGEN(1) ITERATE(25)
/EXTRACTION PC
/ROTATION VARIMAX
/METHOD=CORRELATION.

SPSS FACTOR 输出 I - 总方差解释

在运行我们的第一个因子分析之后，让我们首先检查 Total Variance Explained Table（总方差解释表）（如下所示）。

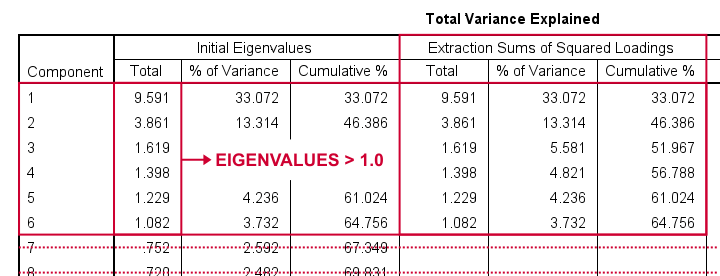
SPSS Factor Output Total Variance Explained

该表告诉我们：

  • SPSS 创建了 29 个称为成分 (components) 的人工变量。
  • 这些成分旨在代表我们分析变量（“条目”）的潜在性格特质。
  • 如果一个成分反映了真实的特质，它应该与这些条目有很大的相关性。或者换句话说：它应该占方差的合理百分比。
  • 像这样，成分 1 占我们 29 个条目方差的 33.07%，相当于 9.59 个条目。这个数字被称为特征值 (eigenvalue)。
  • 因此，您可以将特征值视为成分的“质量分数”：较高的特征值提供更有力的证据表明成分代表真实的潜在特质。现在，最大的问题是：

哪些成分具有足够的特征值被认为是真实的特质？默认情况下，SPSS 对特征值使用 1.0 的截止值。这是因为如果您分析相关性，平均特征值始终为 1.0。因此，这个经验法则完全是任意的：没有真正的理由说明 1.0 应该比 0.8 或 1.2 更好的截止值。

无论如何，SPSS 建议我们的 29 个条目可能衡量了 6 个潜在的特质。我们现在想知道哪些条目衡量了哪些特质。为了回答这个问题，我们检查下面显示的 Rotated Component Matrix（旋转成分矩阵）。

SPSS FACTOR 输出 II - 旋转成分矩阵

Rotated Component Matrix（旋转成分矩阵）包含条目和成分或“因素”之间的 Pearson 相关性。这些被称为因子载荷，使我们能够解释我们的成分可能反映哪些特质。

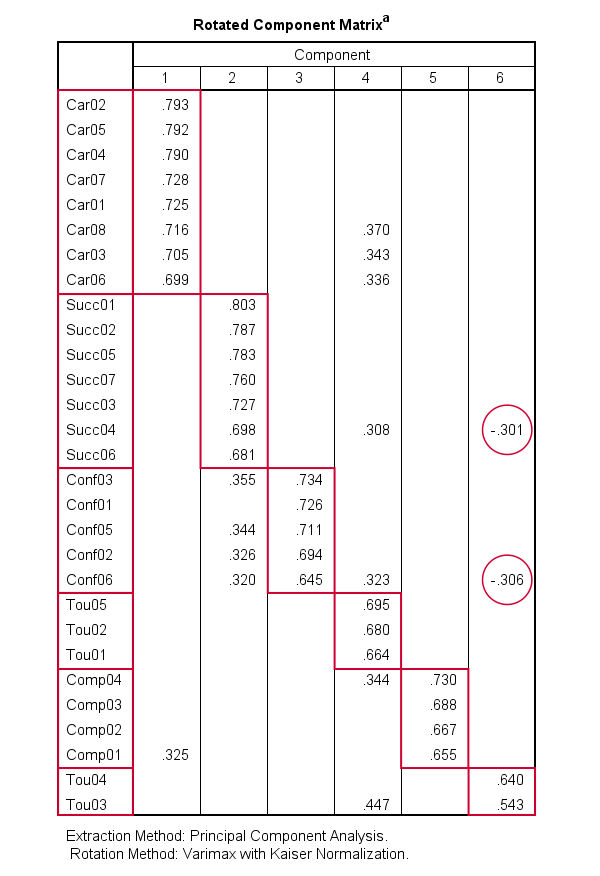
SPSS Factor Output Rotated Component Matrix
  • 成分 1 与 Car02、Car05,…, Car06 强烈相关。如果我们检查这些变量的变量标签，我们看到 “Car” 条目都与 career ambitions（职业抱负） 相关。因此，成分 1 似乎反映了某种职业抱负特质。
  • 成分 2 主要与 “Succ” 条目相关。它们的变量标签告诉我们，这些条目与 successfulness（成功） 相关。
  • 以类似的方式，成分 3 主要与自我 confidence（自信） 条目 Conf01 到 Conf05 相关。
  • 成分 4 似乎衡量了 toughness（坚韧）。
  • 成分 5 可能反映了 competitiveness（竞争力） 特质。
  • 成分 6 与 2 个坚韧条目略微正相关，但与一个成功和自信条目略微_负相关_。由于这些载荷都不是非常强，因此成分 6 不容易解释。

这些结果表明，也许只有成分 1-5 反映了真实的潜在特质。现在，我们刚刚检查的表显示了在我们的 6 个成分（或“因素”）进行 varimax 旋转后的因子载荷。

什么是 Varimax 旋转？

非常基本地说，因子旋转是一种数学过程，它将因子载荷重新分配到各个因子上。这样做的原因是，这使我们的因子更容易解释：旋转通常会导致每个条目恰好在一个因子上具有较高的载荷。有不同的因子旋转方法，但所有这些方法都属于 2 种基本类型：

  • 正交 旋转_不允许_任何因子彼此相关。一个例子是 varimax 旋转。
  • 斜交 旋转允许所有因子彼此相关。例子包括 promax 和 oblimin 旋转。

Factor Rotation Options in SPSS

现在，因子旋转还会重新分配不同因子所解释的方差百分比。新的百分比如下所示在 Rotation Sums of Squared Loadings（旋转平方载荷和）下显示。

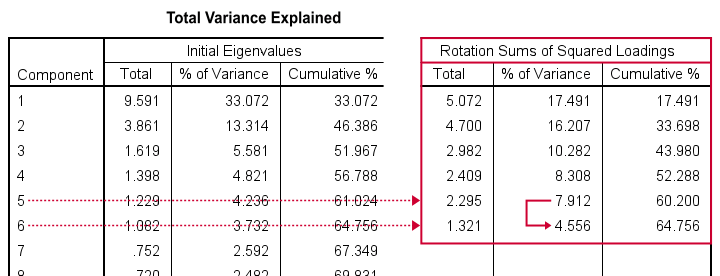
SPSS Factor Output Rotation Sums Of Squared Loadings

这里引人注目的是，从成分 5 (7.91%) 到成分 6 (4.56%) 的巨大下降。这提供了进一步的证据表明，我们的条目可能衡量了 5 个而不是 6 个潜在因素。

因此，我们将重新运行我们的分析，并强制 SPSS 提取和旋转 5 个而不是 6 个因子。我们将通过复制粘贴我们的第一个语法并将 MINEIGEN(1) 替换为 FACTORS(5) 来做到这一点。

SPSS FACTOR 语法 II - 强制 5 因子解

***PCA II - AS PREVIOUS BUT FORCE 5 FACTOR SOLUTION.
**
FACTOR
/VARIABLES Car01 Car02 Car03 Car04 Car05 Car06 Car07 Car08 Conf01 Conf02
Conf03 Conf05 Conf06
Comp01 Comp02 Comp03 Comp04 Tou01 Tou02 Tou03 Tou04 Tou05 Succ01 Succ02 Succ03
Succ04 Succ05 Succ06
Succ07
/MISSING PAIRWISE
/PRINT INITIAL EXTRACTION ROTATION
/FORMAT SORT BLANK(.3)
/CRITERIA **FACTORS(5)** ITERATE(25)
/EXTRACTION PC
/ROTATION VARIMAX
/METHOD=CORRELATION.

结果

我们旋转的成分矩阵现在看起来好多了：每个成分都是可解释的，并且具有一些强的正因子载荷。负载荷都消失了。

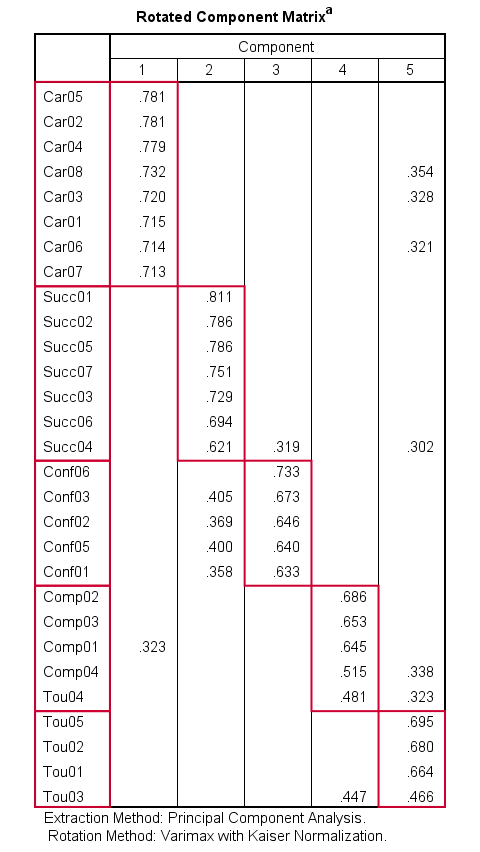
SPSS Factor Output Rotated Component Matrix 5 Factors

Promax 旋转减少交叉载荷

但是，此解决方案的一个问题是，许多条目同时载入 2 个或更多因子。这种次要载荷被称为交叉载荷，与基本因子模型冲突，如下所示。

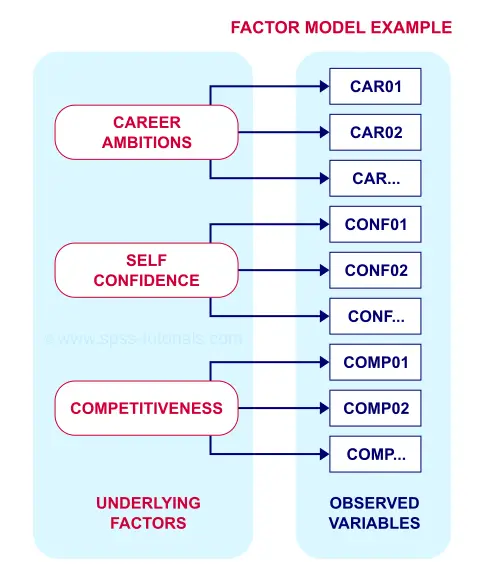
SPSS Factor Analysis Oblique Rotation Example

每个条目仅衡量一个特质，因此应该仅在一个因子上具有实质性的载荷。另请注意，潜在因子之间没有箭头：该模型声称职业抱负、自信和竞争力都完全不相关。是否有人认为这对于现实世界的数据来说是现实的？我当然不这么认为。当然，这些特质是高度相关的。但是，我们的 varimax 旋转不允许我们的因子相关。因此，这些相关性表现为交叉载荷。

对于大多数数据，当我们允许我们的因子相关时，交叉载荷就会消失。我们将通过使用斜交因子旋转（例如 promax）来做到这一点。

SPSS FACTOR 语法 III - Promax 旋转

***PCA III - AS PREVIOUS BUT TRY PROMAX ROTATION.
**
FACTOR
/VARIABLES Car01 Car02 Car03 Car04 Car05 Car06 Car07 Car08 Conf01 Conf02
Conf03 Conf05 Conf06
Comp01 Comp02 Comp03 Comp04 Tou01 Tou02 Tou03 Tou04 Tou05 Succ01 Succ02 Succ03
Succ04 Succ05 Succ06
Succ07
/MISSING PAIRWISE
/PRINT INITIAL EXTRACTION ROTATION
/FORMAT SORT BLANK(.3)
/CRITERIA FACTORS(5) ITERATE(25)
/EXTRACTION PC
/ROTATION **PROMAX**
/METHOD=CORRELATION.

结果

当使用斜交旋转时，我们通常检查 Pattern Matrix（模式矩阵）来解释我们的成分。

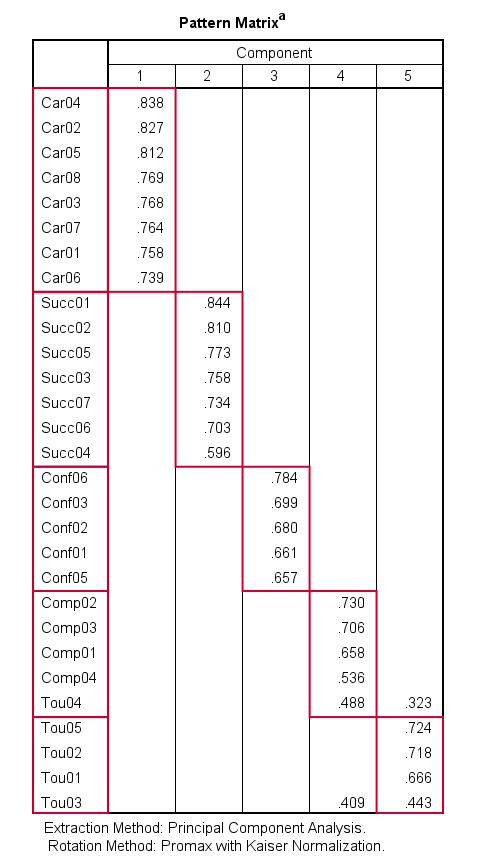
SPSS Factor Pattern Matrix Promax Rotation

我们的模式矩阵看起来很棒！几乎所有的交叉载荷都消失了。但是他们去哪儿了？好吧，因子之间的相关性已经取代了它们的角色。这通常发生在斜交旋转期间。这些相关性显示在 Component Correlation Matrix（成分相关矩阵）中，这是我们输出中的最后一个表。

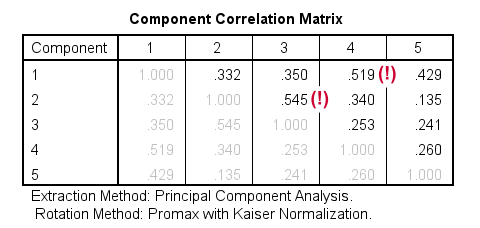
SPSS Factor Promax Rotation Component Correlation Matrix

大多数相关性表明中等甚至强的 效应量。我认为这非常现实：我们的成分反映了诸如成功和自信之类的特质，这些特质在现实世界中显然是高度相关的。

就我个人而言，我倾向于接受此分析提出的变量分组。下一步是检查我们的 5 个子量表的 Cronbach’s alpha。最后，我们将通过 计算平均值 在我们的数据中创建子量表分数，也许可以继续进行 回归分析。

从因子分析中排除条目

大多数教科书建议您现在从分析中排除具有交叉载荷的条目。对于我们的分析，SPSS 显示绝对载荷 < 0.3 为空白。此截止值（尽管完全是任意的）似乎是区分可忽略的载荷和实质性载荷的合理阈值。

无论如何，如果您决定排除条目，正确的做法是：

  • 查找具有最高交叉载荷的变量；
  • 从 FACTOR 语法中删除其变量名；
  • 重新运行因子分析 - 请注意，所有 载荷现在都发生了变化；
  • 如果需要，重复这些步骤并跟踪您正在做的事情。

对于我们的示例分析，这些步骤会产生以下语法。

***PCA IV - AS PREVIOUS BUT REMOVE TOU03.
**
FACTOR
/VARIABLES Car01 Car02 Car03 Car04 Car05 Car06 Car07 Car08 Conf01 Conf02
Conf03 Conf05 Conf06
Comp01 Comp02 Comp03 Comp04 Tou01 Tou02 Tou04 Tou05 Succ01 Succ02 Succ03
Succ04 Succ05 Succ06
Succ07
/MISSING PAIRWISE
/PRINT INITIAL EXTRACTION ROTATION
/FORMAT SORT BLANK(.3)
/CRITERIA FACTORS(5) ITERATE(25)
/EXTRACTION PC
/ROTATION PROMAX
/METHOD=CORRELATION.


***PCA V - AS PREVIOUS BUT REMOVE COMP04.
**
FACTOR
/VARIABLES Car01 Car02 Car03 Car04 Car05 Car06 Car07 Car08 Conf01 Conf02
Conf03 Conf05 Conf06
Comp01 Comp02 Comp03 Tou01 Tou02 Tou04 Tou05 Succ01 Succ02 Succ03 Succ04
Succ05 Succ06
Succ07
/MISSING PAIRWISE
/PRINT INITIAL EXTRACTION ROTATION
/FORMAT SORT BLANK(.3)
/CRITERIA FACTORS(5) ITERATE(25)
/EXTRACTION PC
/ROTATION PROMAX
/METHOD=CORRELATION.


***PCA VI - AS PREVIOUS BUT REMOVE TOU04.
**
FACTOR
/VARIABLES Car01 Car02 Car03 Car04 Car05 Car06 Car07 Car08 Conf01 Conf02
Conf03 Conf05 Conf06
Comp01 Comp02 Comp03 Tou01 Tou02 Tou05 Succ01 Succ02 Succ03 Succ04 Succ05
Succ06
Succ07
/MISSING PAIRWISE
/PRINT INITIAL EXTRACTION ROTATION
/FORMAT SORT BLANK(.3)
/CRITERIA FACTORS(5) ITERATE(25)
/EXTRACTION PC
/ROTATION PROMAX
/METHOD=CORRELATION.

结果

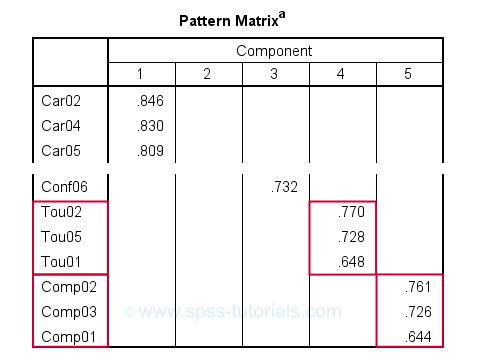
SPSS Factor Analysis Final Pattern Matrix

在删除 3 个具有交叉载荷的条目后，似乎我们有一个完美的因子结构：每个条目似乎仅在一个因子上载入。但是请记住，我们选择抑制绝对载荷 < 0.30。这些没有显示，但它们仍然存在。